CATALOG NO.B37 2010
Ocean Wave

Book fully open

Specifications Edition of 5
15 x 14-1/2 x 2" closed; 15" x 14-1/2" x 45" open.
Multi-panel cut paper 3D model, 14" x 45" open with hard-bound case; multi-color reduction linocut print, 10" x 42"; detailed pamphlet of preparatory drawings.

Collections
Temple University Special Collections Department, Temple University Libraries
Rhode Island School of Design Fleet Library, Special Collections
Swarthmore College, McCabe Library, Special Collections
MIT Libraries Art & Architecture Collection
UC Berkeley Environmental Design Library, Special Collections

This multi-part artist book constructs a virtual ocean wave by using sequential random numbers and a simple mathematical formula. Th>e virtual wave is represented as it would appear in nature from two perspectives: A 3D paper model and a reduction linocut print. The pull-out three-dimensional paper model has thirty-two sequential paper wave cross sections covering an area of 15” x 40”. A 10” x 42” multi-color linocut print is a pictorial representation of the cross sections.

To establish the physical characteristics of this wave, I used data and formulas from a classic work on wave forecasting developed after World War II. Conditions chosen were: 50-knot wind, typical wave height 40 to 50 feet, typical wave length 700 feet, with a ratio of wave length to height of 15 to 1. The 3D paper model is constructed at a scale of 1= 300 or 1” = 25 feet. The linocut print image is based on the 3D model and augmented using written descriptions of actual wind conditions as well as reference photographs from the Beaufort Wind Scale. However, the linocut image does not exist in photographic form.

Deriving the wave shape All wave forms are sequential objects defined by a series of points moving through space and time creating an oscillating motion and a periodic repetition of the basic wave form.
Since ocean waves are basically sinusoidal, I derived the virtual wave by using a sine function with a random number component. This produced an irregular sine wave approximating what might exist in nature (fig. 1.)

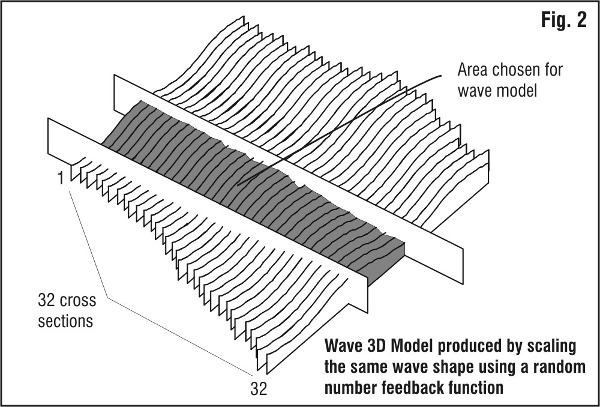
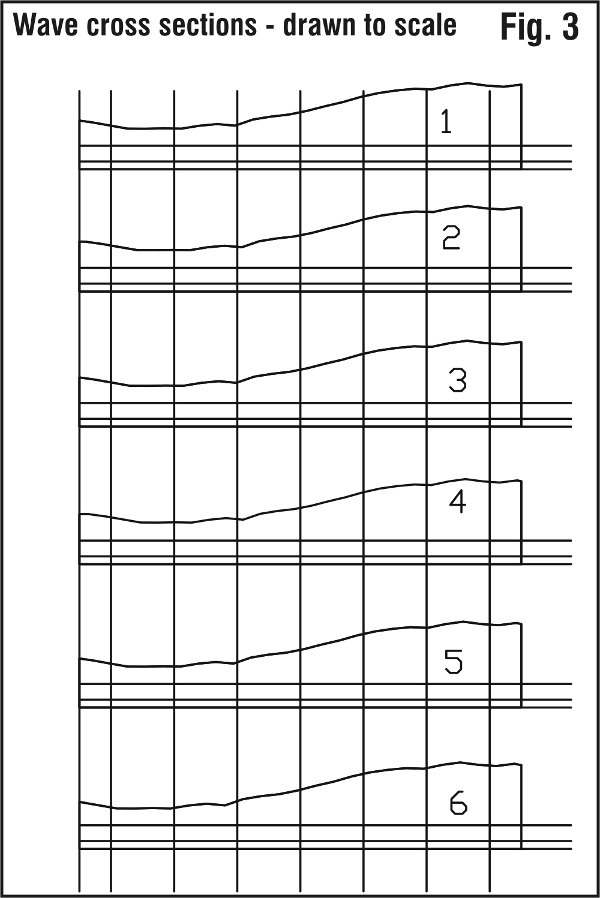
Creating the sequence of wave cross sections Using the principles of self similarity in nature I used a simple feedback function to create a sequence of cross sections of the original wave shape (fig. 1) at different relative scales. I used 3D CAD software to draw a 3D computer model of the wave (fig. 2) and chose an area of this 3D computer model for the paper model. I printed the thirty-two individual cross sections and modified them, by hand, to produce the slight alterations that actual wind conditions would produce (fig. 3). I then used a saw to cut the sections out of the paper and assemble the model. The result: 32 cross sections, in sequence, form a three dimensional representation of the wave.

Case open wave model partially extended

Case closed

3 panel print

Detail view